西江月·证明
即得易见平凡,仿照上例显然。
留作习题答案略,读者自证不难。
反之亦然同理,推论自然成立。
略去过程Q.E.D.,由上可知证毕。
就是后缀数组。
主要由两个数组组成,s a [ i ] sa[i] s a [ i ] i i i r k [ i ] rk[i] r k [ i ] i i i s a [ r k [ i ] ] = r k [ s a [ i ] ] = i sa[rk[i]]=rk[sa[i]]=i s a [ r k [ i ] ] = r k [ s a [ i ] ] = i
我们可以在 O ( l o g n ) O(log\ n) O ( l o g n )
我们这里会利用倍增的思想去实现。
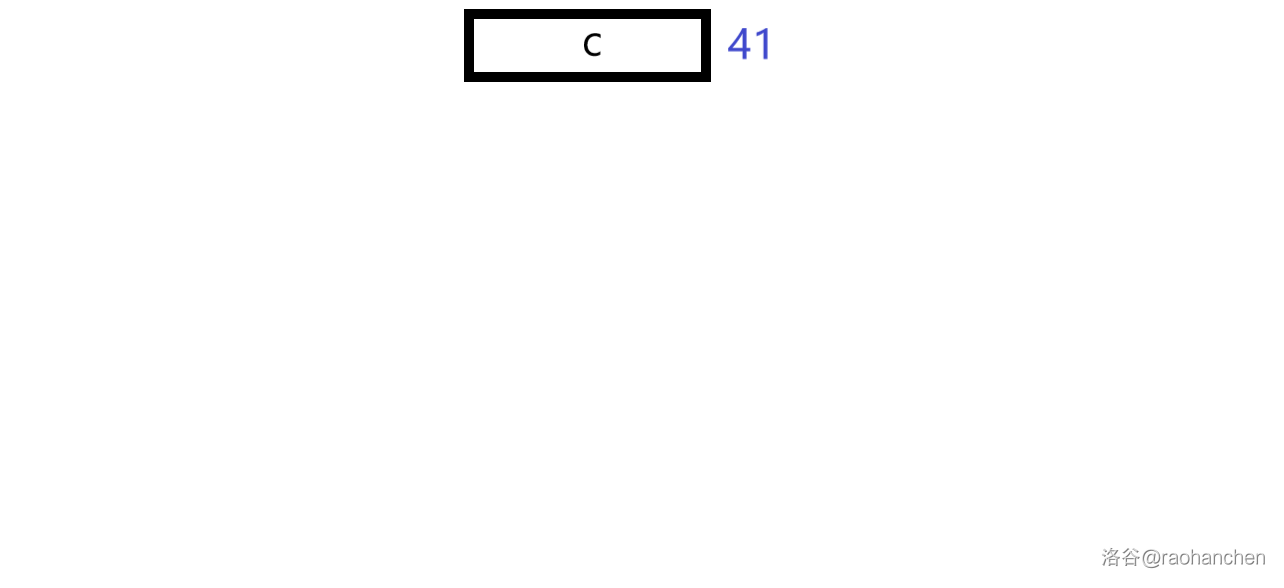
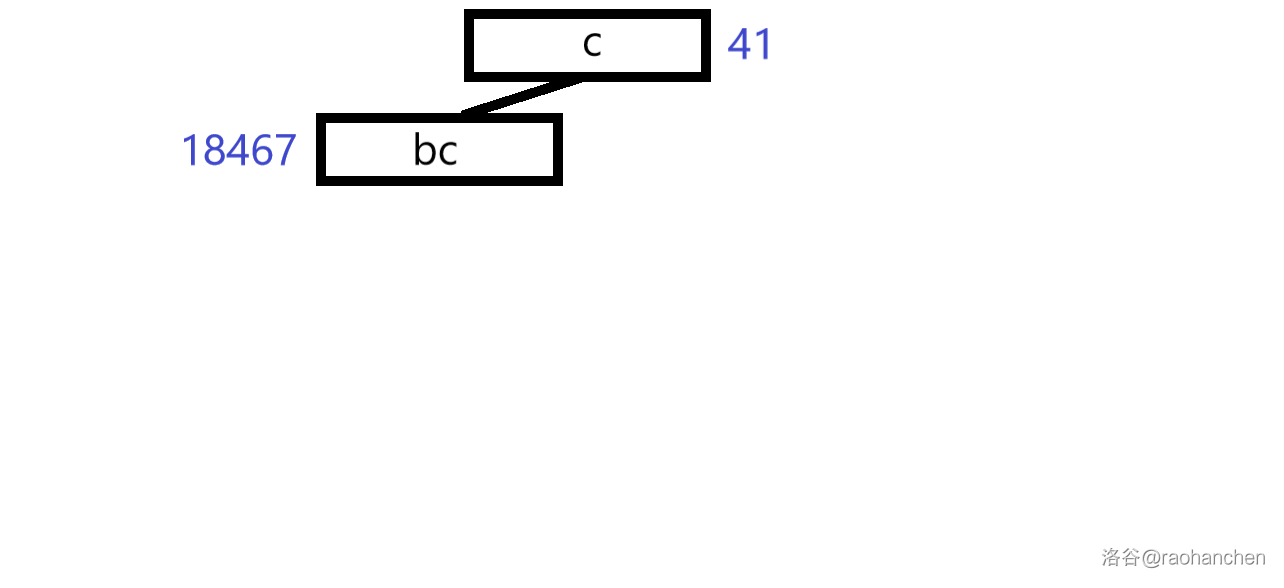
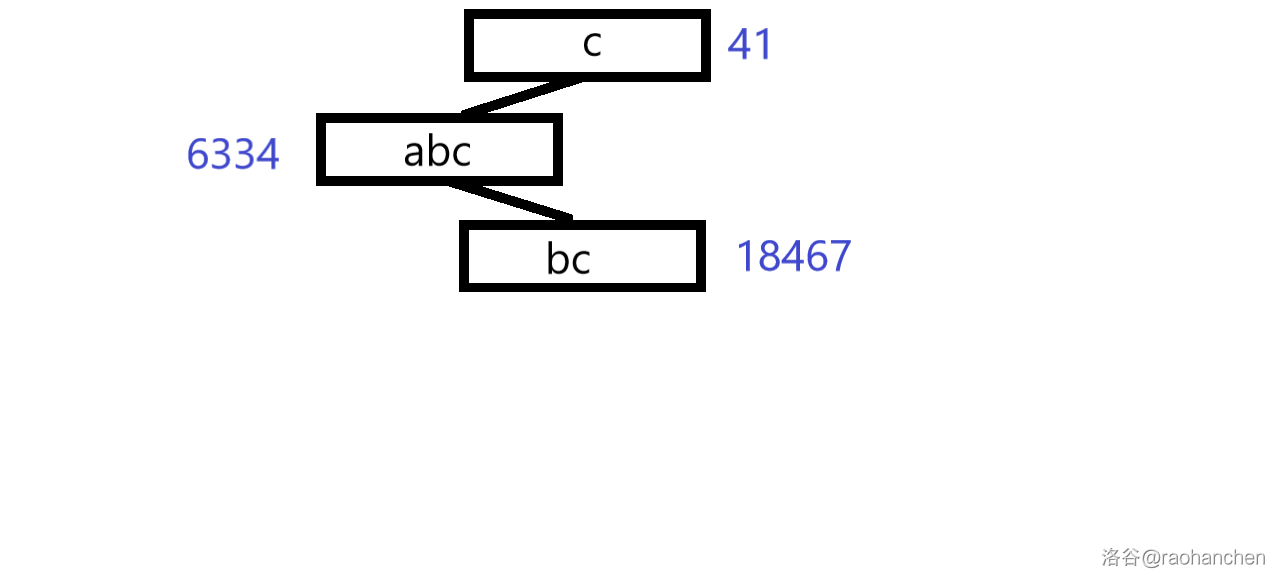
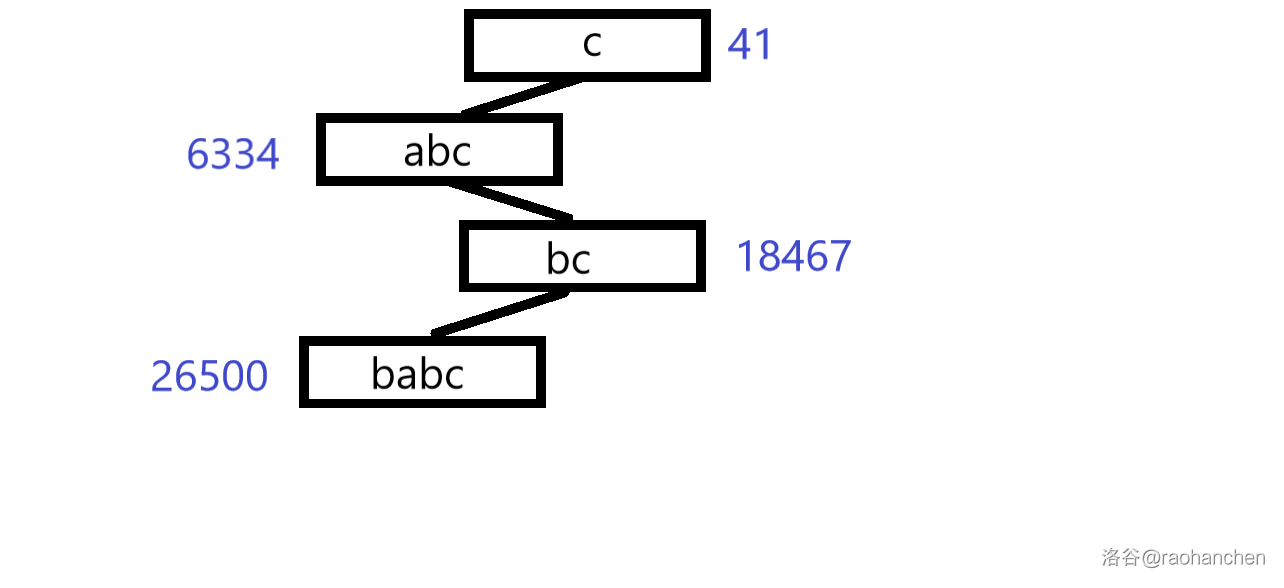
这里就用一个经典老图来描述一下过程
本质上也就是一个双关键字排序的过程。
如果我们是用sort排序的话就会退化成O ( n l o g 2 n ) O(nlog^2n) O ( n l o g 2 n ) o ( n ) o(n) o ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 const int Maxn = 1000010 ;int n;char s[Maxn];int sa[Maxn], rk[Maxn], oldrk[Maxn << 1 ];int id[Maxn], px[Maxn], cnt[Maxn];inline bool cmp (int x, int y, int w) return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];inline void work () int i, m = 300 , p, w;scanf ("%s" , s + 1 );strlen (s + 1 );for (i = 1 ; i <= n; ++i)for (i = 1 ; i <= m; ++i)1 ];for (i = n; i >= 1 ; --i)for (w = 1 ;; w <<= 1 , m = p)for (p = 0 , i = n; i > n - w; --i)for (i = 1 ; i <= n; ++i)if (sa[i] > w)memset (cnt, 0 , sizeof (cnt));for (i = 1 ; i <= n; ++i)for (i = 1 ; i <= m; ++i)1 ];for (i = n; i >= 1 ; --i)memcpy (oldrk, rk, sizeof (rk));for (p = 0 , i = 1 ; i <= n; ++i)cmp (sa[i], sa[i - 1 ], w) ? p : ++p;if (p == n)for (int i = 1 ; i <= n; ++i)break ;for (i = 1 ; i <= n; ++i)printf ("%d " , sa[i]);int main () work ();return 0 ;
当然还有更牛逼的 O ( n ) O(n) O ( n )
关于应用的话,比如说在字符串中快速找到子串,显然的一个性质就是若是子串,必定是原串的某些后缀中的前缀。
我们就可以利用这个性质来去二分地查找位置,做到O ( ∣ S ∣ l o g ∣ T ∣ ) O(|S|log\ |T|) O ( ∣ S ∣ l o g ∣ T ∣ )
并且,我们在求出了后缀数组之后可以利用它的性质求出一些其他有用的数组来帮助我们维护一些奇怪的东西。
这里我们定义 $ height[i]=lcp(sa[i],sa[i-1]) $,也就是说第 i i i
那么咋求出来?只需要一个定理: $height[rk[i]] \ge height[rk[i-1]]-1 $。
那么我们就可以 O ( n ) O(n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 for (int i=1 ,k=0 ;i<=n;i++)if (rk[i])if (k) while (s[i+k]==s[sa[rk[i]-1 ]+k)
既然我们求出来了这个数组,它就一定有它特别的用处,即应用。
可以用来求LCP:
显然 l c p ( s a [ i ] , s a [ j ] ) = m i n ( h e i g h t [ i + 1... j ] ) lcp(sa[i],sa[j])=min(height[i+1...j]) l c p ( s a [ i ] , s a [ j ] ) = m i n ( h e i g h t [ i + 1 . . . j ] )
可以用来比较同一字符串中两子串的大小关系:
假设我们需要比较 A = S [ a . . b ] A=S[a..b] A = S [ a . . b ] B = S [ c . . d ] B=S[c..d] B = S [ c . . d ] A < B ⇔ r k [ a ] < r k [ c ] A<B \Leftrightarrow rk[a]<rk[c] A < B ⇔ r k [ a ] < r k [ c ]
也可以用来求不同的子串的数目:
子串也就是后缀的前缀。那么我们可以美剧每一个后缀,计算它的前缀总数量,最后在减去重复的。
可以用来求出现至少k次的子串的最大长度:
也就是后缀排序中至少有连续k k k k − 1 k-1 k − 1 h e i g h t height h e i g h t o ( n ) o(n) o ( n )
可以用来判断是否有某文本串不重叠地出现了至少两次:
可以直接二分目标地的长度,并将 h e i g h t height h e i g h t s s s
除此之外,它还可以解决有关连续的若干个相同子串的问题,详情可见 [NOI2016] 优秀的拆分。
关于这题,显然AABB是由两个形如AA的串拼起来的,所以我们考虑去维护两个数组a a a b b b a [ i ] a[i] a [ i ] i i i b [ i ] b[i] b [ i ] i i i
那么最终解为$\sum\limits_{i=1}^{n-1}a[i]b[i+1] $。
我们就只需要考虑怎么把这两个数组求出来即可。
显然可以 o ( n 2 ) o(n^2) o ( n 2 ) i i i j j j
我们考虑去枚举一个 l e n len l e n l e n ∗ 2 len*2 l e n ∗ 2
我们每隔着一个 L e n Len L e n a , b a,b a , b
那么先求出来这对相邻点所代表前缀的最长公共后缀 L C S LCS L C S L C P LCP L C P L C P LCP L C P L C S LCS L C S L C P + L C S − L e n + 1 LCP+LCS-Len+1 L C P + L C S − L e n + 1
所以我们就可以直接差分了,复杂度为 O ( n l o g n ) O(nlog\ n) O ( n l o g n )
代码就不放了因为我没写。
可以在 O ( n ) O(n) O ( n )
它以高度压缩的形式存在,是一张有向无环图的形式,包含了关于字符串 s s s t 0 t_0 t 0 s s s s s s t 9 t_9 t 9
那么我们可以称任意一条路径对应 了它标号所构成的字符串。由于到达某个状态的路径不止一条,我们说一个状态对应了一些字符串的集合,而这个集合的每个元素会单独对应这些路径。
定义说完了,构建可以看OI-Wiki
一种用来维护字符串后缀的数据结构,是把所有后缀按照字典序排序后构建出来的平衡树。
我们先尝试着离线构造一棵这样的树。
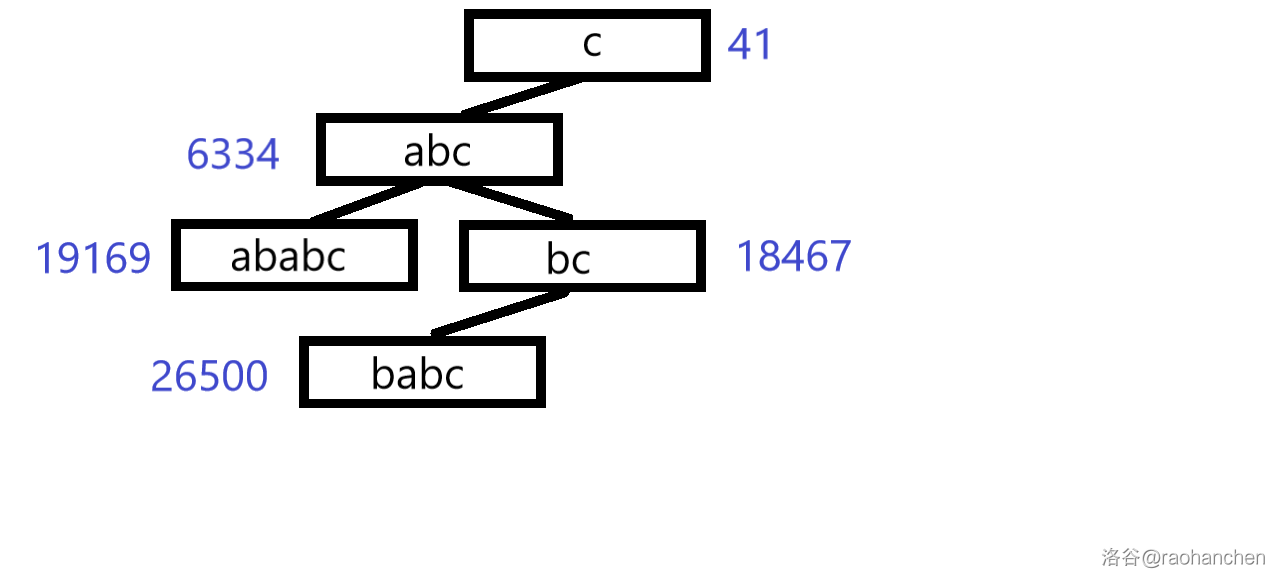
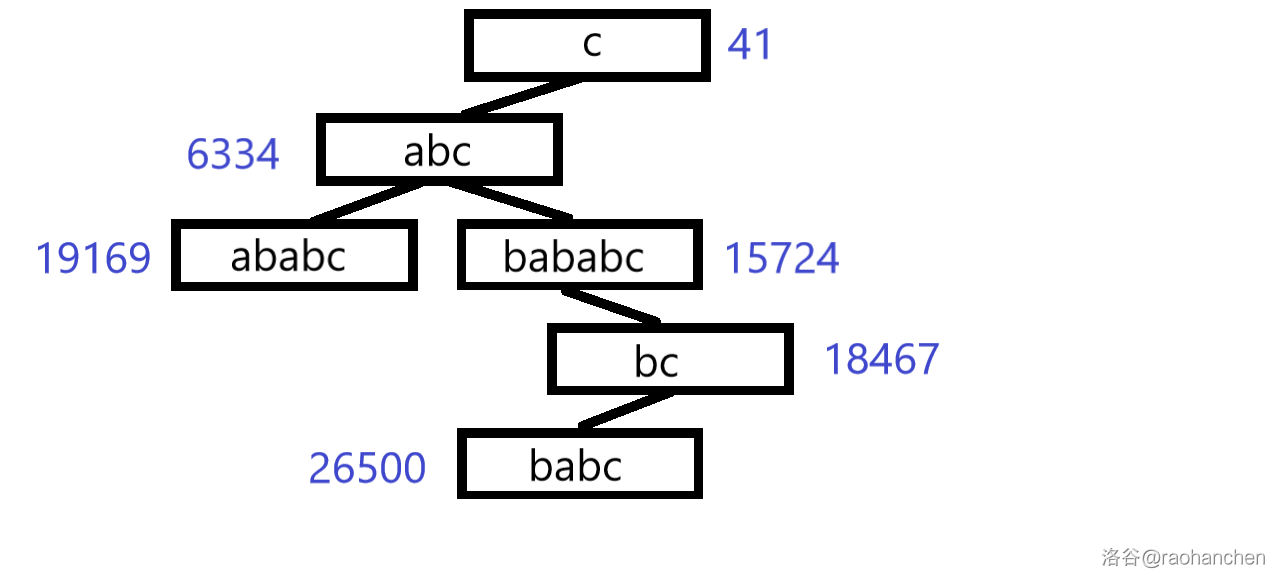
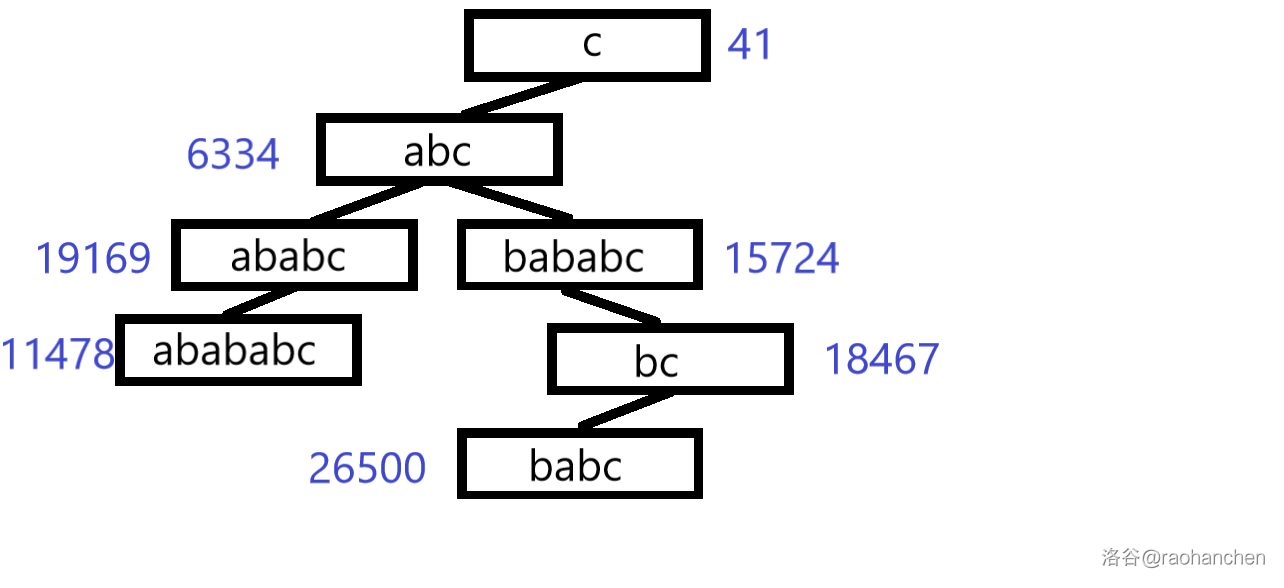
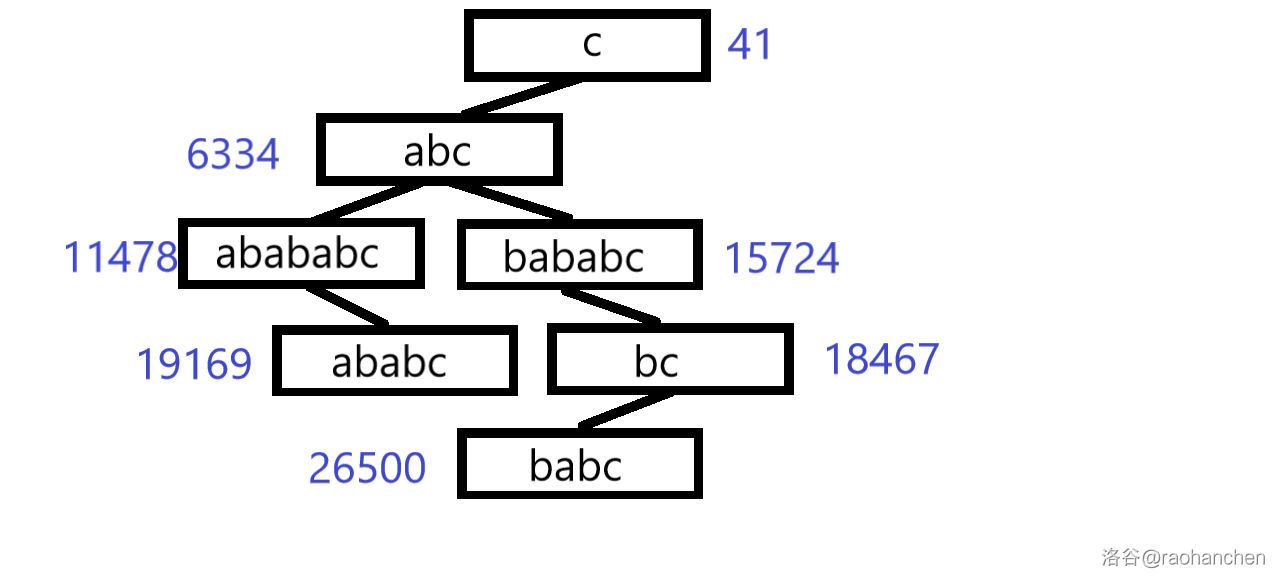
设我们有字符串 a b a b a b c abababc a b a b a b c a b a b a b c abababc a b a b a b c a b a b c ababc a b a b c a b c abc a b c b a b a b c bababc b a b a b c b a b c babc b a b c b c bc b c c c c
然后对着一个序列怎么给他弄成平衡树?替罪羊树很好的告诉了我们答案,二分把它拎起来就行。
但是我们这种做法还是需要提前求出来后缀数组,时间复杂度为 O ( n ) o r O ( l o g n ) O(n)\ or\ O(log\ n) O ( n ) o r O ( l o g n )
那么我们再考虑在线构造。
那就把后缀一个一个地插入平衡树即可。
我们遍历到每一个节点的时候,用即将插入的后缀 x x x y y y x > y x>y x > y
我们这里用Treap作为基本模板。
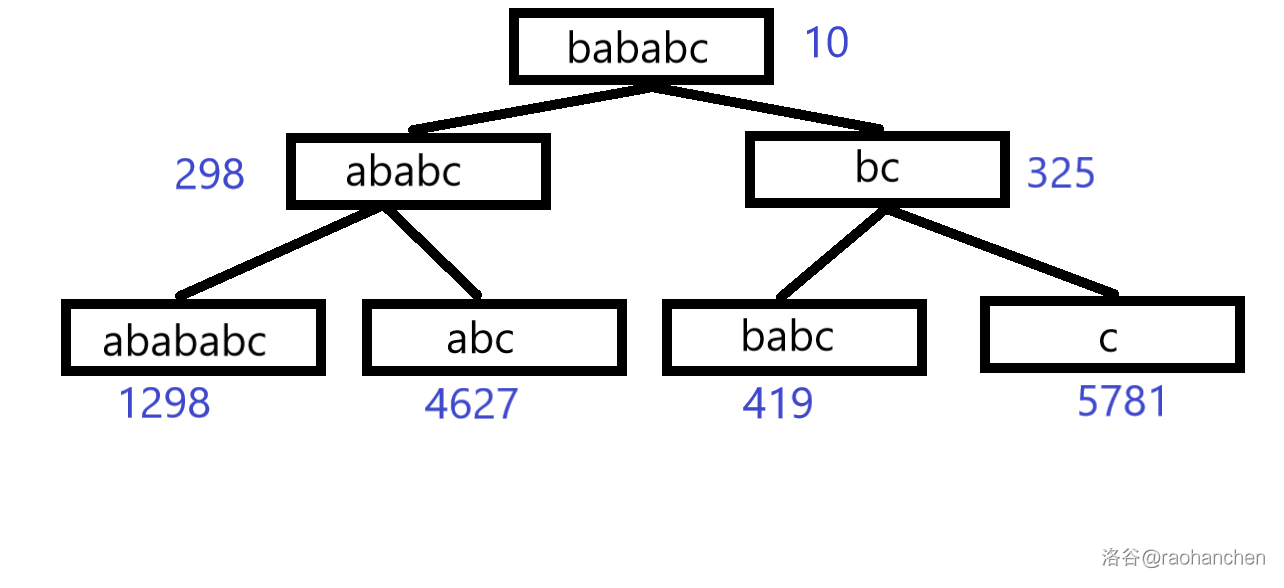
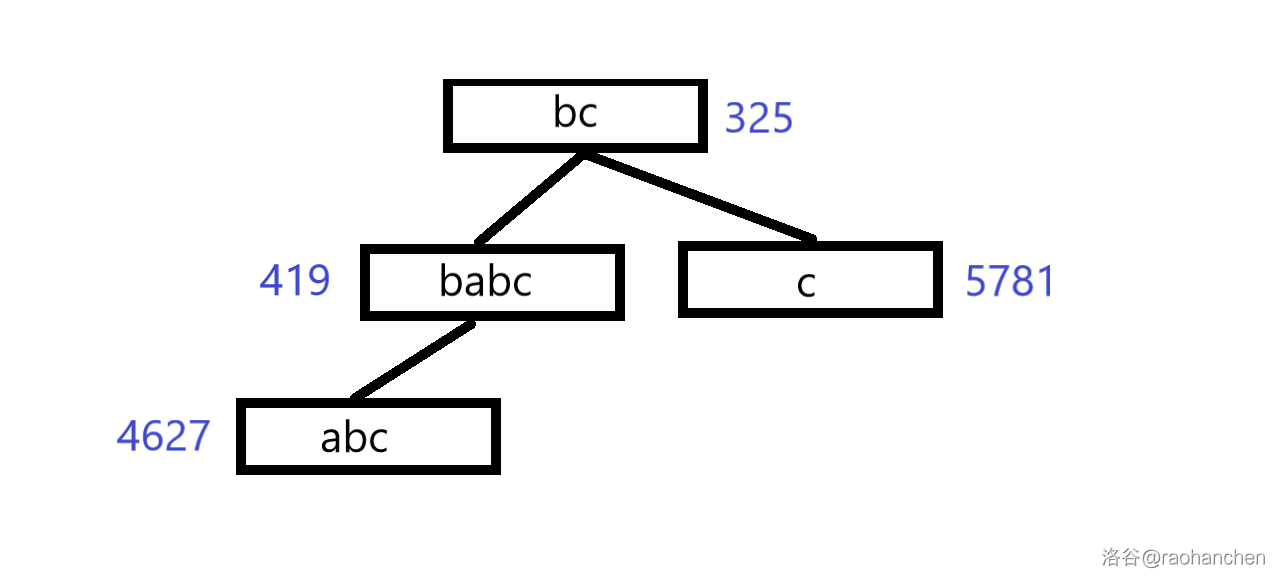
然后我去网上偷了图,我们在这里模拟一下 a b a b a b c abababc a b a b a b c
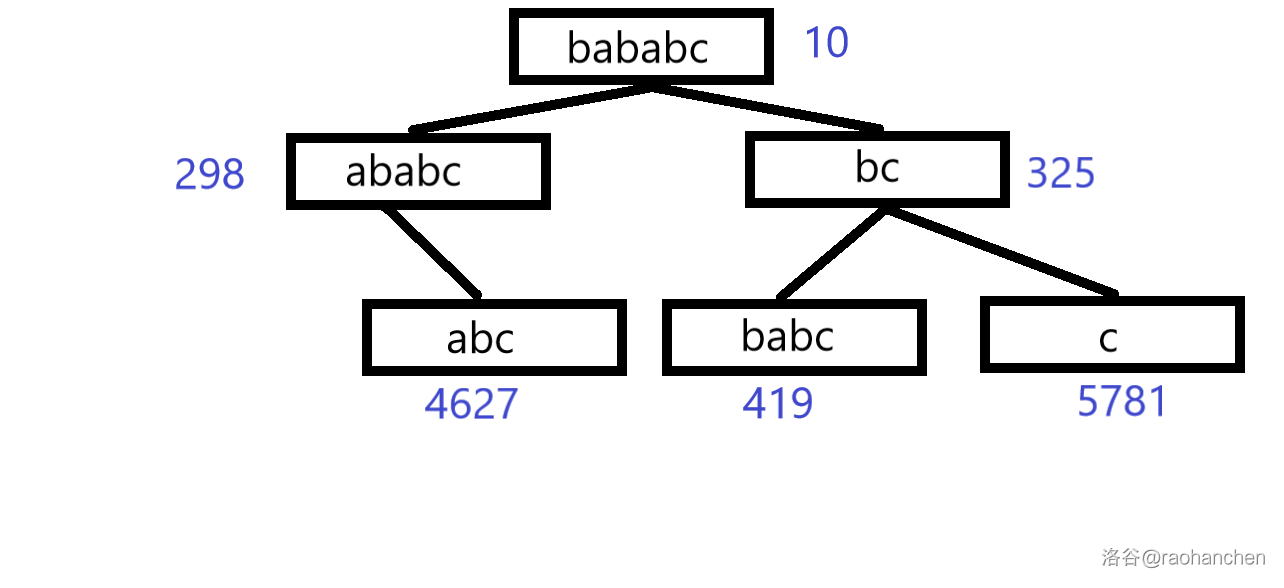
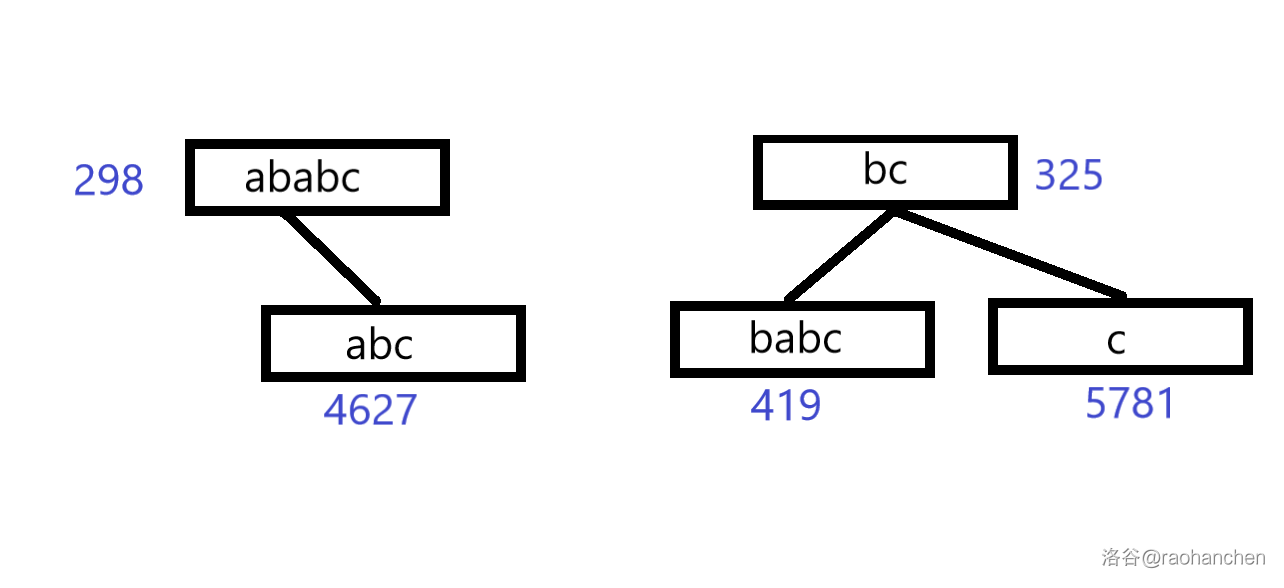
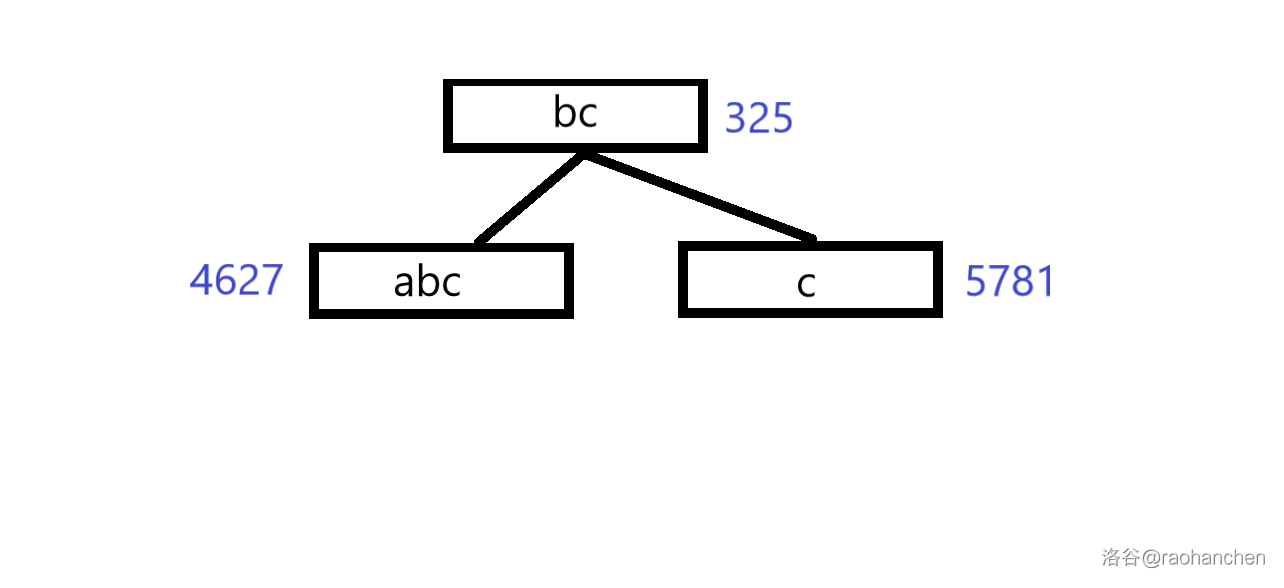
与之相对应的,它也支持删除操作。再整一个例子,我们把它的后缀一个一个删除。
原图:a b a b a b c abababc a b a b a b c b a b a b c bababc b a b a b c
完事之后就这样:
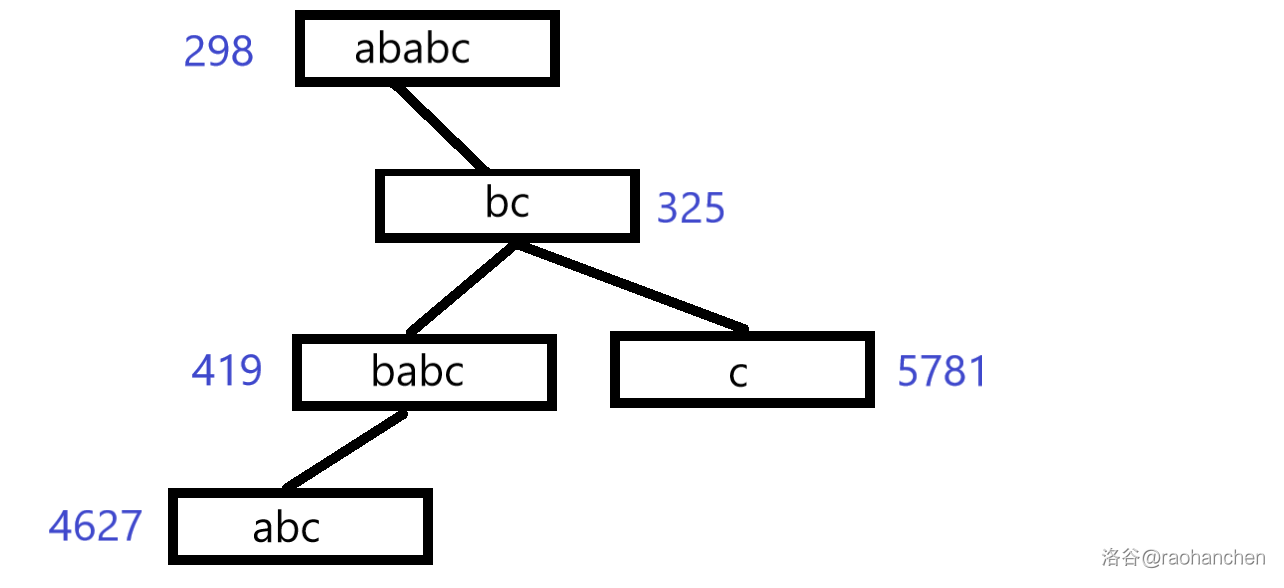
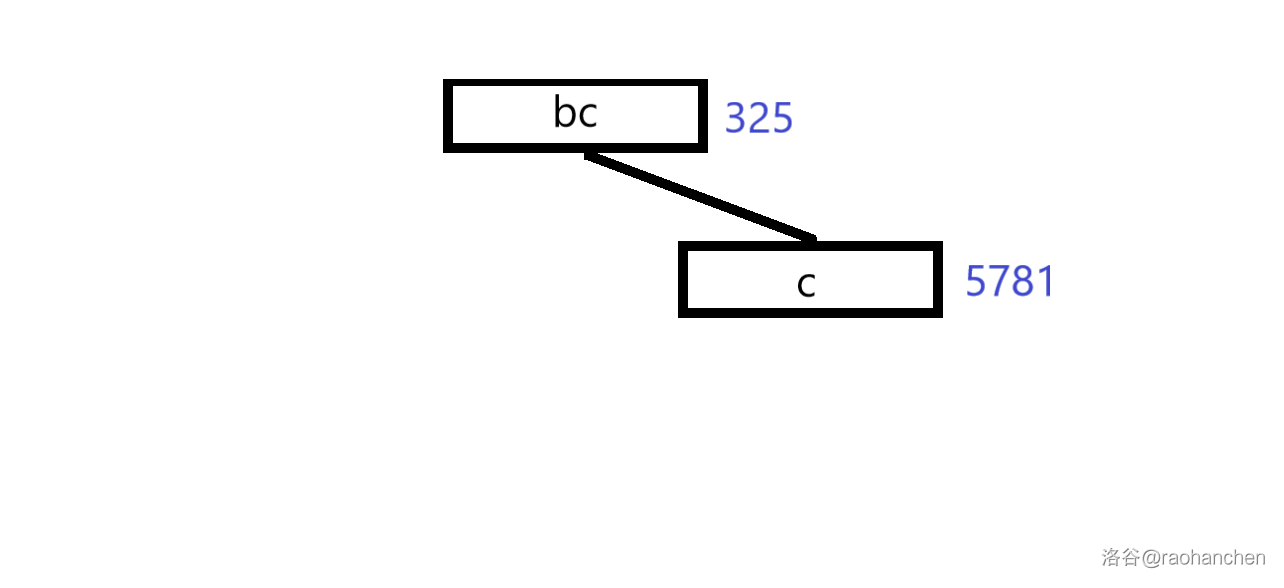
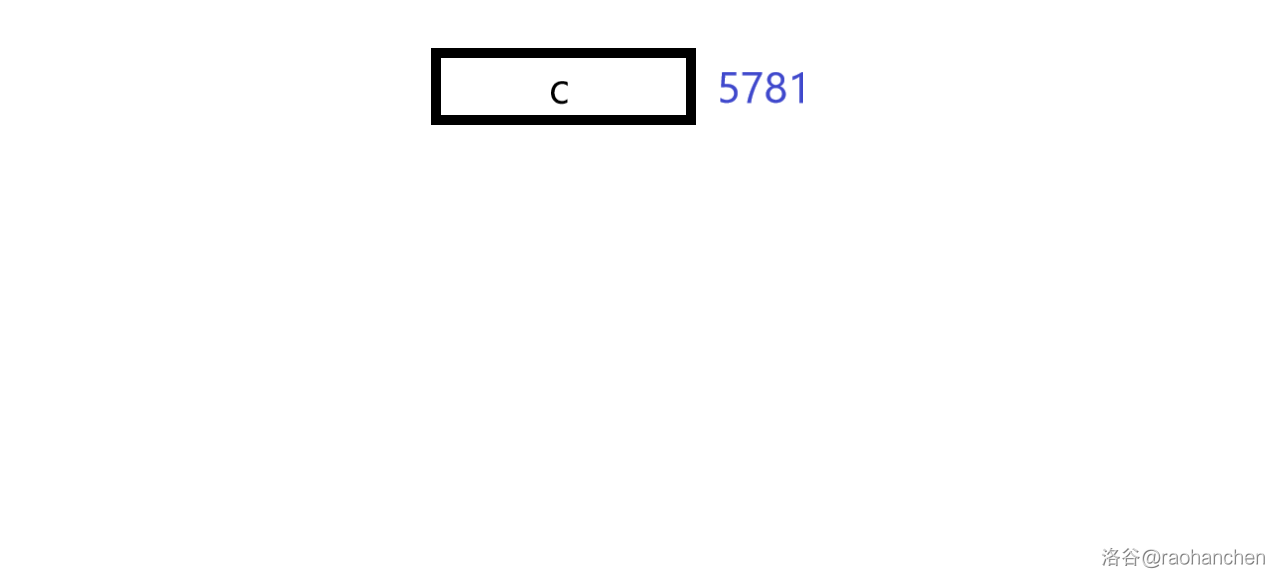
3.删 a b a b c ababc a b a b c b a b c babc b a b c a b c abc a b c b c bc b c c c c
那么后缀平衡树就可以动态地插入、删除一个后缀辣!
但是我们操作的是后缀,所以我们只是可以在一个字符串前插入或者删除一个字符。与之相对的,后缀自动机是在后面插入一个字符。
当然,它本质上还是个平衡树,你会写平衡树就会写,所以并不难掌握。
我们由普通的平衡树插入入手,给他做一些修改。
我们普通平衡树一般需要去维护 s i z e , c n t , v a l , k e y size,cnt,val,key s i z e , c n t , v a l , k e y v a l val v a l
但是我们只关心字典序大小来比较即可,那么我们可以把每个点的编号设置为当前后缀开始的位置,比如节点 1 1 1 1 1 1
那么代码可以这样写:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 inline void ins (int &i, int p) if (!i)rand ();1 ;1 ;return ;if (comp (i, p) > 0 )ins (trp[i].ls, p);up (i);if (trp[i].key > trp[trp[i].ls].key)zig (i);else if (comp (i, p) < 0 )ins (trp[i].rs, pos);pushup (i);if (trp[i].key > trp[trp[i].rs].key)zag (i);
那么我们还剩下个问题:怎么去写两个后缀的比较函数捏?
我们当然可以暴力比较,但是很劣。
我们想要的是 O ( 1 ) O(1) O ( 1 )
现在我们的任务是在已经插入完毕的字符串 S S S x x x x S xS x S S S S
我们重新定义每个点的权值 v a l val v a l v a l val v a l
大概代码实现是这样的
1 2 3 4 5 6 7 8 9 inline int comp (int x, int y) if (s[x] > s[y] or s[x] == s[y] and trp[x + 1 ].val > trp[y + 1 ].val)return 1 ;else if (s[x] == s[y] and trp[x + 1 ].val == trp[y + 1 ].val)return 0 ;else return -1 ;
那么现在我们解决了一个问题,但是又创造出了一个新问题: v a l val v a l
我们当然可以直接前驱和后继取个平均值来算,但是这样会有精度问题。也就是说如果我们插入后缀是单调上升的,你构造出来的树就会是偏心的。
那么我们基于这个东西优化一下。我们发现上面的方法中会使权值构造出来一棵并不平衡的树,考虑利用它的性质来完成我们构建真正的平衡树。
就像线段树一样,传 l , r l,r l , r ( l + r ) > > 1 (l+r)>>1 ( l + r ) > > 1 l , ( ( l + r ) > > 1 ) − 1 l, ((l+r)>>1)-1 l , ( ( l + r ) > > 1 ) − 1 ( l + r ) > > 1 , r (l+r)>>1,r ( l + r ) > > 1 , r
但是每一次旋转会改变权值,不是吗?
那么我们可以去利用“重量平衡树”的方法去平衡。也就是说,在进行了插入或者删除操作之后,为了保证树的平衡而重构子树大小为均摊或者说期望 O ( l o g n ) O(log\ n) O ( l o g n )
那么,我们每一次插入都需要用 O ( l o g n ) O(log\ n) O ( l o g n ) O ( l o g n ) O(log\ n) O ( l o g n ) 那么就是多了个小常数罢了
那么代码也就可以写出来了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 inline void get_val (int p, long long l, long long r) if (!p)return ;1 ;get_val (trp[p].ls, l, trp[p].val - 1 );get_val (trp[p].rs, trp[p].val + 1 , r);inline void zig (int &p, long long l, long long r) int q = trp[p].ls;up (p), up (q);get_val (q, l, r);inline void zag (int &p, long long l, long long r) int q = trp[p].rson;pushup (p);pushup (q);get_val (q, l, r);void ins (int &i, int p, long long l, long long r) if (!i)rand ();1 ;1 ;1 ;return ;if (comp (i, p) > 0 )ins (trp[i].ls, pos, l, trp[i].val - 1 );up (i);if (trp[i].key > trp[trp[i].ls].key)zig (i, l, r);else if (comp (i, p) < 0 )ins (trp[i].rs, p, trp[i].val + 1 , r);up (i);if (trp[i].key > trp[trp[i].rs].key)zag (i, l, r);return ;
删除同理,这里用FHQ的做法去合并,就不用分类讨论了。那么合并后只需要重构即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 inilne int merge (int x, int y) if (!x || !y)return x | y;if (trp[x].key < trp[y].key)merge (trp[x].rs, y);up (x);return x;else merge (x, trp[y].ls);up (y);return y;void del (int &i, int p, long long l, long long r) if (!i)return ;if (comp (i, p) == 0 )if (trp[i].cnt > 1 )else merge (trp[i].ls, trp[i].rs), get_val (i, l, r);pushup (i);return ;if (comp (i, p) > 0 )del (trp[i].ls, p, l, trp[i].val - 1 );else del (trp[i].rs, p, trp[i].val + 1 , r);up (i);return ;
那么后缀平衡树的插入与删除我们就知道了。
怎么让它做后缀数组的活呢?
你建立完之后你会发现dfs一遍就可以求出来S A SA S A s a , r k sa,rk s a , r k
还是有代码
1 2 3 4 5 6 7 8 9 10 int cnt;inline void dfs (int i) if (!i)return ;dfs (trp[i].ls);dfs (rtp[i].rs);return ;
总的来说后缀平衡树就是 S A SA S A S A SA S A
它的代码相对来说更长,但是由于有了平衡树的前身,它并不难懂也并不难写。
没了。
这俩是一个东西=_=虽然我以前一直不知道
是可以在O ( n ) O(n) O ( n )
自动机的结构都差不多,回文自动机也是由转移边与f a i l fail f a i l
又由于回文串的长度存在奇数和偶数两种,那么我们肯定不能直接建在一棵树上,所以我们考虑建两棵树来分别存储这两种不同的回文串。
那么我们就考虑去记录下来两棵树的两个根,也就是奇根与偶根。那么我们一般限定偶根编号为0 0 0 0 0 0 f a i l fail f a i l 1 1 1 1 1 1 f a i l fail f a i l
那么我们再说说f a i l fail f a i l
先说一下结论,一个点的f a i l fail f a i l
我们再加入一个新的字符的时候,我们需要从当前的节点不断地去跳f a i l fail f a i l
那么新建节点的长度一定是等于这个节点的长度加上2 2 2 f a i l fail f a i l
一个新节点肯定是在它父节点的某一个回文后缀的两侧各拓展一个字符所得到的,所以新建节点后,我们可以从它父亲的f a i l fail f a i l
我们在这里再特殊的看一下两个根的f a i l fail f a i l 1 1 1 f a i l fail f a i l
而如果跳到的是奇根,那么肯定是可以向两侧拓展的,所以奇根的f a i l fail f a i l
那么就可以直接看代码啦:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #define Maxn 2000010 struct node int fail, num, lens; int ch[26 ];int n, len, lst, cnt, s[Maxn];char c[Maxn];inline void init () 0 ].lens = 0 , t[1 ].lens = -1 ;0 ].fail = 1 , t[1 ].fail = 0 ;0 , cnt = 1 ;return ;inline int gtfail (int i) while (s[n - t[i].lens - 1 ] != s[n])return i;inline void ins () int i = gtfail (lst);if (!t[i].ch[s[n]])2 ;int v = gtfail (t[i].fail);1 ;int k;inline void work () init ();scanf ("%s" , c + 1 );strlen (c + 1 );0 ] = 26 ;for (n = 1 ; n <= len; n++)97 + k) % 26 + 97 ;'a' ;ins ();printf ("%d " , t[lst].num);return ;int main (void ) work ();return 0 ;
那么这就是回文自动机的板子啦
是求出字符串的最小表示的算法。
什么是最小表示?即为一个字符串首尾拼接后你随意找一个点断开,要求断开之后形成的字符串的字典序最小。
我们可以在 O ( n ) O(n) O ( n )
首先把这个字符串复制一遍放在原串的后面。
我们一开始搞两个指针 i i i j j j s [ 0 ] s[0] s [ 0 ] s [ 1 ] s[1] s [ 1 ] k = 0 k=0 k = 0 s [ i + k ] s[i+k] s [ i + k ] s [ j + k ] s[j+k] s [ j + k ] k + + k++ k + +
如果整个字符串的长度都没有找到不相等的位置,那么证明整个字符串都是相等的字符,那么那个位置就是最小表示的位置,直接返回即可。
显然,全过程中 s [ i + k ] s[i+k] s [ i + k ] s [ j + k ] s[j+k] s [ j + k ]
1.当 s [ i + k ] > s [ j + k ] s[i+k]>s[j+k] s [ i + k ] > s [ j + k ] s [ i ] − s [ i + k − 1 ] s[i] - s[i+k-1] s [ i ] − s [ i + k − 1 ] i i i i + k + 1 i+k+1 i + k + 1
2.当 s [ i + k ] < s [ j + k ] s[i+k]<s[j+k] s [ i + k ] < s [ j + k ] j j j j + k + 1 j+k+1 j + k + 1
3.当 s [ i + k ] = s [ j + k ] s[i+k]=s[j+k] s [ i + k ] = s [ j + k ] k + + k++ k + +
那么如果改变指向后 i = j i=j i = j i , j i,j i , j
也就是如果 k = l e n k=len k = l e n l e n len l e n m i n ( i , j ) min(i,j) m i n ( i , j )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 const int Maxn = 3e5 + 10 ;int n;int a[Maxn * 2 ];int ansx;int i, j = 1 , k;inline void work () read ();for (register int i = 0 ; i < n; i++)read ();while (i < n and j < n and k < n)if (a[(i + k) % n] == a[(j + k) % n])else if (a[(i + k) % n] > a[(j + k) % n])1 ;else 1 ;if (i == j)0 ;min (i, j);for (register int i = 0 ; i < n; i++)printf ("%d " , a[(i + ansx) % n]);return ;
这东西用处的话。。。主要还是用它的性质去做一些最优性选择之类的,当然你也可以来判断两个字符串是不是本质相同。
当然了你也可以直接去用SA来做捏。
冷门。
我们先下个定义:Lyndon串,我们定义为字符串本身就是所有后缀中字典序最小的。
而Lyndon分解,就是把字符串按照顺序不重叠地划分为 m m m s i ≥ s i + 1 s_i\ge s_{i+1} s i ≥ s i + 1
那么其实Lyndon分解可以直接利用后缀数组求解:首先,s m s_m s m s a [ 1 ] sa[1] s a [ 1 ] s m − 1 + s m s_{m-1}+s_m s m − 1 + s m s m s_m s m r k = i rk=i r k = i r k rk r k
那么这个做法的复杂度是跟后缀数组复杂度挂钩的。
重新考虑一种做法。
给出引理:1. 如果a a a b b b a b ab a b
2.如果字符串a a a c c c a c ac a c c c c d d d a d ad a d
证明的话我可能口胡,也可能由于一些原因而导致不证明,我们现在就把他当作一个前提条件。
可以在 O ( n ) O(n) O ( n ) i , j , k i,j,k i , j , k i i i [ 1 , i − 1 ] [1,i-1] [ 1 , i − 1 ]
那么就去维护一个循环不变式,也就是说保持这个式子在循环的过程中始终为真。
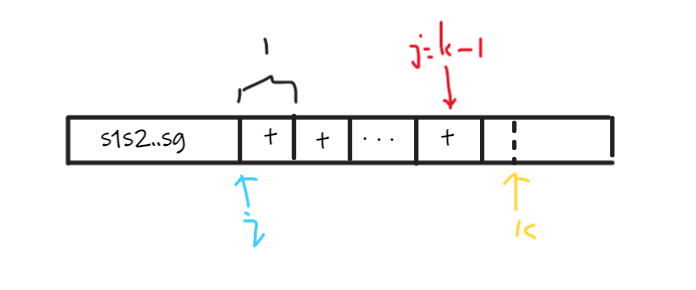
为 $ s[1,i-1]=s_1s_2s_3…sg, \forall l \in [1,g],s_l \in Lyndon $ 串且 s l > s l + 1 sl>s{l+1} s l > s l + 1
$ s[i,k-1] = t^h + v(h>1) $ 为不固定的分解,并且满足 v v v t t t
大体的关系就是这样子:
我们当前读入的字符为 s [ k ] s[k] s [ k ] j = k − ∣ t ∣ j=k-|t| j = k − ∣ t ∣
$ s[k]=s[j] $,那么 $ k++,j++ $
$ s[k]>s[j] $,由引理2可得 $ s[k]+v $为Lyndon串,那么又由于Lyndon分解有字典序限制,那么我们就不断向前合并,最终会得到 $ t^h+v+s[k] $ 为一个新的符合条件的Lyndon串。
$ s[k]<s[j]> , t^h $ 的分解就被固定下来,而算法就会直接从 v v v
最终我们可以得到一个 $ O(n) $的做法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <bits/stdc++.h> using namespace std;#define Maxn 100010 * 50 int n, ansx;char s[Maxn];inline void work () scanf ("%s" , s + 1 ), n = strlen (s + 1 );for (int i = 1 ; i <= n;)int j = i, k = i + 1 ;while (k <= n and s[j] <= s[k])while (i <= j)1 , i += k - j;printf ("%d" , ansx);return ;int main (void ) work ();return 0 ;
没了。
我们称形如一个字符串复制一遍之后放在它本身后边形成的新字符串为重串。
我们的目标是找到给定字符串中的所有重串,或者,我们解决一个更简单的问题:我们找到一个字符串中的任意一个重串或者最长的一个重串。
我们在开始之前首先界定一下,S ˉ \bar{S} S ˉ S S S
一个字符串s s s
这里还会有一些关于重串数量的结论:
若是一个重串的原串并不是重串,那么我们称这个串为本原重串,并且可以证明的是,本源重串最多只有 n l o g n nlogn n l o g n
若是我们把一个重串用一个三元组 $ (i,p,r) $ 进行压缩,且其中 i i i p p p r r r n l o g n nlogn n l o g n
我们发现斐波那契字符串具有高度周期性。对于一个长度为 n i n_i n i s i s_i s i
核心是分治。
这个算法是把字符串划分为左右两个部分,首先计算完全处于字符串左部或者右部的重串数量,然后再计算起始位置在左部,终止部分在右部的重串数量。这个算法的关键点在于求交叉重串的数量,我们在下面去探讨。
我们记一个字符除按左部为u u u v v v s = u + v s=u+v s = u + v u , v u,v u , v s s s s [ i . . . j ] s[i...j] s [ i . . . j ] u u u
那么我们接下来考虑如何找到所有的左偏重串。
我们会记录左边重串长度为 2 l 2l 2 l v v v u u u u [ p ] u[p] u [ p ]
那么就把 p p p c a c a d a cac\ ada c a c a d a p = 1 p=1 p = 1 c a c a caca c a c a
那么我们一旦固定住了 p p p l l l p p p
即使固定住了 p p p
我们记录 l e n 1 len_1 l e n 1 s [ p − 1 ] s[p-1] s [ p − 1 ] l e n 2 len_2 l e n 2 s [ p ] s[p] s [ p ]
所以我们可以给出某个长度为 $ 2l=2(l_1+l_2)=2(|u|-p) $ 的子串为重串的充要条件:
我们设 $ k_1 $ 为满足 $ u[p-k_1,…p-1]=u[|u|-k_1…|u|-1] $ 的最大整数,而 $ k_2 $ 为满足 $ u[p…p+ k_2-1]=v[0…k_2-1] $ 的最大整数,那么对于任意满足 $ l_1\le k_1,l_2\le k_2 $ 的二元组来说,我们都可以恰好找到一个与之对应的重串。
所以我们考虑怎么计算 k 1 , k 2 k_1,k_2 k 1 , k 2
k 1 k_1 k 1 u ˉ \bar{u} u ˉ k 2 k_2 k 2 ’+u $ 的Z函数,而’ '所代表的是 u , v u,v u , v
右偏重串就和求左偏重串的方法几乎一致了,这里感兴趣的可以看OI-Wiki ,不再阐述。
实现的话如果你只想找一个重串,时间复杂度为O ( n l o g n ) O(n\ log\ n) O ( n l o g n ) O ( n 2 ) O(n^2) O ( n 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 vector<int > z_function (string const &s) int n = s.size ();vector<int > z (n) ;for (int i = 1 , l = 0 , r = 0 ; i < n; i++)if (i <= r)min (r - i + 1 , z[i - l]);while (i + z[i] < n && s[z[i]] == s[i + z[i]])if (i + z[i] - 1 > r)1 ;return z;int get_z (vector<int > const &z, int i) if (0 <= i && i < (int )z.size ())return z[i];else return 0 ;int , int >> repetitions;void convert_to_repetitions (int shift, bool left, int cntr, int l, int k1, int k2) for (int l1 = max (1 , l - k2); l1 <= min (l, k1); l1++)if (left && l1 == l)break ;int l2 = l - l1;int pos = shift + (left ? cntr - l1 : cntr - l - l1 + 1 );emplace_back (pos, pos + 2 * l - 1 );void find_repetitions (string s, int shift = 0 ) int n = s.size ();if (n == 1 )return ;int nu = n / 2 ;int nv = n - nu;substr (0 , nu);substr (nu);string ru (u.rbegin(), u.rend()) ;string rv (v.rbegin(), v.rend()) ;find_repetitions (u, shift);find_repetitions (v, shift + nu);int > z1 = z_function (ru);int > z2 = z_function (v + '#' + u);int > z3 = z_function (ru + '#' + rv);int > z4 = z_function (v);for (int cntr = 0 ; cntr < n; cntr++)int l, k1, k2;if (cntr < nu)get_z (z1, nu - cntr);get_z (z2, nv + 1 + cntr);else 1 ;get_z (z3, nu + 1 + nv - 1 - (cntr - nu));get_z (z4, (cntr - nu) + 1 );if (k1 + k2 >= l)convert_to_repetitions (shift, cntr < nu, cntr, l, k1, k2);